
Double-blind randomised controlled trials (RCTs) are the gold standard for evaluating clinical interventions in the biomedical field. A defining feature of RCTs is that of randomisation, the statistical process whereby participants are assigned to different treatment groups according to a predefined random mechanism. Whether the mechanism is simple or complex, the rationale remains the same – to uphold the scientific rigor essential for generating unbiased, credible, and generalisable clinical evidence. This article provides a comprehensive guide to randomisation in clinical trials, exploring its fundamental principles, various methods, and the practical challenges involved. A detailed case study will be used to illustrate how these concepts are applied in practice to achieve reliable and impactful outcomes.
The Importance of Randomisation
The process of randomisation strengthens the reliability and validity of clinical evidence by preventing selection bias, which occurs when differences in participant characteristics influence treatment assignment. Selection bias may result in population samples that are not representative of the population of interest and can also lead to systematic differences between treatment groups. If the trial population is not representative of the population intended to benefit from the investigational treatment, then the results of the trial will not be generalisable. And if systemic differences between treatment groups cause an imbalance in either known or unknown variables that are associated with study endpoints then the observed effects of treatment might be distorted due to confounding bias.
Randomisation also plays a crucial role in facilitating double blinding in clinical trials, a design where both participants and investigators are unaware of treatment assignment. While randomisation does not inherently create blinding, it ensures that treatment allocation cannot be predicted based solely on a participant's baseline characteristics. Randomisation is also an ethical and transparent approach to treatment assignment, promoting fairness by giving each participant an equal chance of assignment. Furthermore, the assumption of random treatment assignment also underpins many robust statistical methods that are essential for reliable and valid inference.
Types of Randomisation Mechanisms
Modern randomisation practices go beyond simply flipping a coin. Researchers use advanced statistical techniques and tools to implement randomisation schemes that meet the specific needs of a trial. These can range from simple methods, such as random number generation, to more complex strategies, such as stratified or block randomisation, which account for specific variables or constraints. Below are the main types of randomisation commonly employed in clinical research:
-
Simple Randomisation
Simple randomisation is the most straightforward approach. Participants are assigned to treatment groups purely at random, typically using tools such as random number generators. While simple randomisation is effective for large trials, in smaller studies it can lead to imbalances in group sizes or characteristics, potentially affecting the validity of results.
-
Block Randomisation
Block randomisation ensures that treatment groups remain balanced at predefined intervals throughout the allocation process. The first step of block randomisation is to determine block sizes, which must be a multiple of the smallest number of participants required to achieve the predetermined proportion or participants in each treatment group. For example, block sizes for a simple trial with two arms of equal size should be a multiple of 2. The next step is to generate all possible arrangements of group assignment within the block. For example, in a block of size 4 with two groups (A and B), possible arrangements could include AABB, ABAB, BBAA or BABA. One arrangement is then randomly selected, and participants are assigned to groups sequentially based on this pre-randomised order. To further increase unpredictability, several different block sizes may be used within the same trial. This method is particularly useful for maintaining balance when patient enrolment is staggered over time.
-
Stratified Randomisation
Stratified randomisation accounts for specific variables – such as age, gender, or baseline health conditions – that could influence treatment outcomes. Participants are grouped into strata based on these variables, and randomisation occurs within each stratum. This method reduces the risk of confounding and ensures a balanced distribution of key characteristics across groups.
-
Complex Randomisation
Complex randomisation refers to methods that go beyond the straightforward randomisation techniques discussed above. These methods are typically employed when trials have specific needs, such as unequal allocation ratios, multiple treatment arms, or stratification by multiple factors, and aim to address challenges that arise in such scenarios. For example, unequal allocation ratios may be used to gather more data on experimental treatments, to address ethical concerns or to account for higher anticipated dropout rates in one group to maintain statistical power.
Complex randomisation methods also include data driven approaches such as minimisation and adaptive randomisation. Minimisation aims to minimise imbalances between treatment groups by adjusting allocation probabilities in real time to favour the treatment group that leads to a greater improvement in balance. Adaptive randomisation also adjusts allocation probabilities in real time, but the aim is instead to favour the treatment group that appears to have greater efficacy. These randomisation strategies are beyond the scope of this article.
Key Considerations for Effective Randomisation
Successful implementation of randomisation in clinical trials requires careful attention to both logistical and technical details. Key considerations include planning and documentation of the randomisation process, protecting the integrity of allocation data, handling emergency unblinding and maintaining robust quality control and archiving practices. This ensures alignment with the current ICH E6(R2) guidelines on good clinical practice, an international ethical and scientific quality standard for designing, conducting, recording and reporting trials that involve the participation of human subjects.
-
Panning and Documentation
Effective randomisation begins with a detailed plan that addresses all trial-specific requirements. This involves defining treatment allocation ratios, stratification factors, block sizes, and the number of study centres. Collaborating closely with clients during this phase ensures alignment on critical elements, such as the format and delivery of randomisation outputs and any client-specific needs, such as drug kit lists or third-party integrations. Developing a dummy randomisation schedule provides stakeholders with a clear preview of the final outputs while maintaining blinding, reducing the risk of errors. Proper planning and thorough documentation set the foundation for a seamless randomisation process and help avoid costly adjustments later in the trial.
-
Maintaining Confidentiality and Integrity
Preserving the confidentiality of randomisation data is critical to ensuring the integrity of clinical trials by maintaining treatment blinding. Randomisation schedules should be stored in secure electronic systems with restricted access, allowing only authorized personnel to view or retrieve the information. Data transfers must be encrypted and password-protected, with passwords shared securely and separately. To prevent bias, the team responsible for generating the randomisation must operate independently from those involved in data analysis and reporting. Robust access controls, clear documentation, and adherence to best practices ensure that the integrity of the randomisation process is upheld throughout the trial.
-
Emergency Unblinding Protocols
Emergency unblinding protocols are essential to handle critical situations, such as serious adverse events (SAEs), while minimizing the impact on the trial's integrity. Procedures should allow for controlled, individual unblinding without revealing the treatment allocation for the entire study. Secure systems must be in place to enable quick access to unblinded information by authorized personnel, such as site investigators, without compromising the study’s overall blinding. Clear guidelines and training for site staff and stakeholders ensure that emergency unblinding is conducted appropriately and documented thoroughly. These protocols balance participant safety with the need to preserve the trial's scientific rigor.
-
Quality Control and Archiving
Thorough quality control (QC) processes are essential to ensure that randomisation schedules are accurate and aligned with trial specifications. Every randomisation schedule should undergo rigorous QC checks, including validation of software-generated outputs and verification against the randomisation specifications. Once finalised, all randomisation-related materials—including schedules, programming files, and QC documentation—must be securely archived in electronic formats. Proper labelling and metadata ensure these materials are easily identifiable and accessible only to authorized personnel. While electronic storage is the primary method, supplementary hard copies may be maintained as a backup. By prioritizing robust QC and secure archiving, trials safeguard the integrity and reliability of their randomisation processes.
Managing the Complexities of Multi-Centre Trials
Modern clinical trials are often conducted across several sites, introducing additional complexities to the randomisation processes. Consistency across sites is essential to maintain trial integrity and prevent bias. Effective management of multi-centre trials relies heavily on the use of centralised randomisation systems to maintain consistency and rigor across all locations. Platforms such as Interactive Response Technology (IRT) or Interactive Web Response Systems (IWRS) enable real-time, automated randomisation while adhering to the trial’s specific design requirements. These systems ensure treatment allocation remains uniform, even across geographically dispersed sites, and reduce the risk of manual errors or deviations. Centralized randomisation also allows for streamlined integration of stratification factors, ensuring balance within individual sites and across the entire trial. By centralising this process, trial managers can monitor and oversee randomisation in a cohesive, standardised manner.
Stratification and blocking are also critical in multi-centre trials to ensure balanced treatment groups and control variability across sites. Stratifying randomisation by centre helps address potential differences in patient populations or site-specific factors that could impact outcomes. Block randomisation further ensures that treatment assignment remains evenly distributed within each site. To preserve the integrity of the trial, block sizes should be carefully planned but not disclosed to site personnel. Incorporating these design elements during the planning phase lays a strong foundation for a trial that is both scientifically robust and operationally seamless.
Unequal Allocation Ratios
Unequal allocation in clinical trials is the intentional assignment of participants to treatment groups in differing proportions (e.g., 2:1 or 3:1). While unequal allocation can negatively affect the statistical power of a trial, its advantages often justify this trade-off when carefully planned and executed. Common reasons for using unequal allocation include:
- To gather more comprehensive data and improve the precision of estimates in the experimental treatment group.
- To address ethical considerations, such as minimising the number of participants exposed to a potentially less effective treatment when there is evidence against clinical equipoise.
- To accommodate differences in costs between treatment groups, optimising resource allocation.
- To account for anticipated differences in drop-out rates between groups, which can help maintain statistical power in per-protocol analyses. (Dumville, 2006)
Despite these advantages, trials with unequal allocation are underutilised, making up only 2.3% of studies in the MEDLINE database from 1991-1995 (Avins, 1998).
Randomisation in Practice: A Case Study
To demonstrate the practical implementation of a complex randomisation mechanism, I will use an example from a statistical consultancy project that involved designing a phase II proof-of-concept trial with five treatment arms and unequal allocation ratios. Three of the arms were varying doses of the active compound [low (L), mid (M) and high (H)], one of the arms was a positive control (PC) and the final arm was a negative control (NC). Randomisation occurred at two sites, stratified by both site and a binary baseline characteristic (BL), in a 3:3:3:2:2 ratio respectively. Sample size calculations determined that 234 (54:54:54:36:36) participants were required to maintain adequate statistical power. Additionally, the randomisation mechanism had to be designed so that the allocation ratio of 3:3:3:2:2 was adhered to as closely as possible for a 50% interim analysis. To achieve this, a tailored version of stratified block randomisation was implemented.
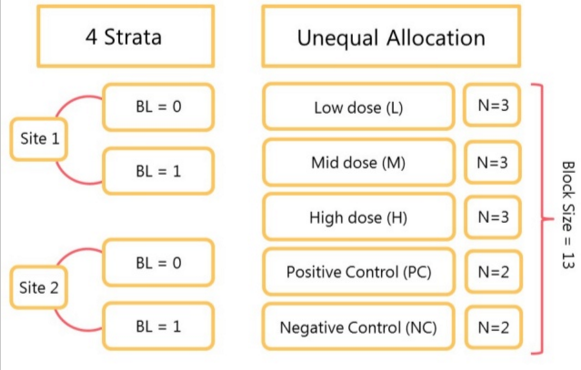
Treatments L, M, H, PC and NC in 3:3:3:2:2 allocation ratio gives a block size of 13 (3+3+3+2+2). The main block of 13 was then divided into the following 3 sub-blocks:
- 1:1:1:1:1 – one participant is assigned to each treatment (L, M, H, PC, NC).
- 1:1:1:1:0 – one participant is assigned to treatments L, M, H, and PC, but no participant is assigned to NC.
- 1:1:1:0:1 - 1 participant is assigned to treatments L, M, and H, and to NC, but no participant is assigned to PC.
Two levels of randomisation were utilised. The order of each treatment (L, M, H, PC and NC) was randomised within each sub-block, and the order of the sub-blocks was randomised within the main block (ABC, ACB, BAC, BCA, CAB, CBA). Although not possible using the client’s standard in-house randomisation systems, this randomisation mechanism was straightforward to program in SAS. The final randomisation was then uploaded into the client system. The randomisation lists made provision for 234 participants within each stratum to account for the possibility that only one of the four strata was able to recruit. The lists were then cascaded to the pharmacies at each site, where treatment was prepared for administration as and when required (minimising overage).
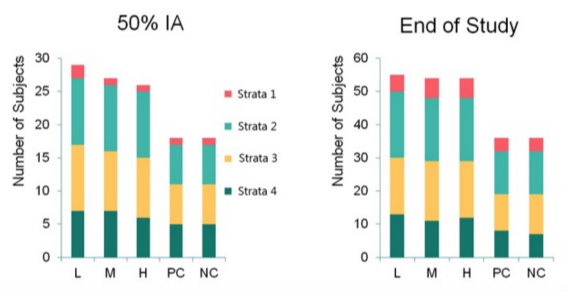
This case study demonstrates that seemingly complex designs with unequal allocation ratios can be broken down into more manageable chunks. The randomisation mechanism described above ensured that at any snapshot in time the observed allocation ratio approximated the expected ratio. The observed allocation ratios at the 50% interim analysis (IA) and end of study analysis are shown in the figure below.
Conclusion
Randomisation is a fundamental component of clinical trial design. This article has highlighted the importance of randomisation in mitigating bias, facilitating blinding, and upholding ethical standards in treatment allocation. From simple to complex mechanisms, the choice of randomisation method depends on the trial's unique requirements and challenges. Effective implementation requires meticulous planning, robust quality control and a commitment to maintaining data confidentiality and integrity. By embracing innovative approaches and utilising advanced technologies, researchers are able to navigate the logistical challenges of randomisation and ensure that clinical trials generate reliable and generalisable evidence. Ultimately, a well-executed randomisation strategy is instrumental in advancing medical science and improving patient outcomes.
Request a Consultation
References
- Avins, AL. 1998. Can unequal be more fair? Ethics, subject allocation, and randomised clinical trials. J Med Ethics; 24:401-408.
- Dumville JC, et al. 2006. The use of unequal randomisation ratios in clinical trials: a review. Contemp. Clin. Trials; 27(1): 1-12

!['Clinical Trial Transparency and ALLTrials' by Ben Goldacre [Video]](https://www.quanticate.com/hs-fs/hub/22135/file-2523594494.jpg?width=390&name=file-2523594494.jpg)
