
Bayesian statistics in clinical trials are becoming more widely used in the pharmaceutical industry. By gathering data from historical studies, it is possible to reduce the sample size of the current trial by using an informative prior in the Bayesian analysis. This blog explores five cases in different indications that have historical data on placebo subjects from the literature, and calculates the effective sample size using an informative prior. In some cases, the effective sample size is substantial, but in others there are no sample size savings despite abundant data in the literature.
Methods
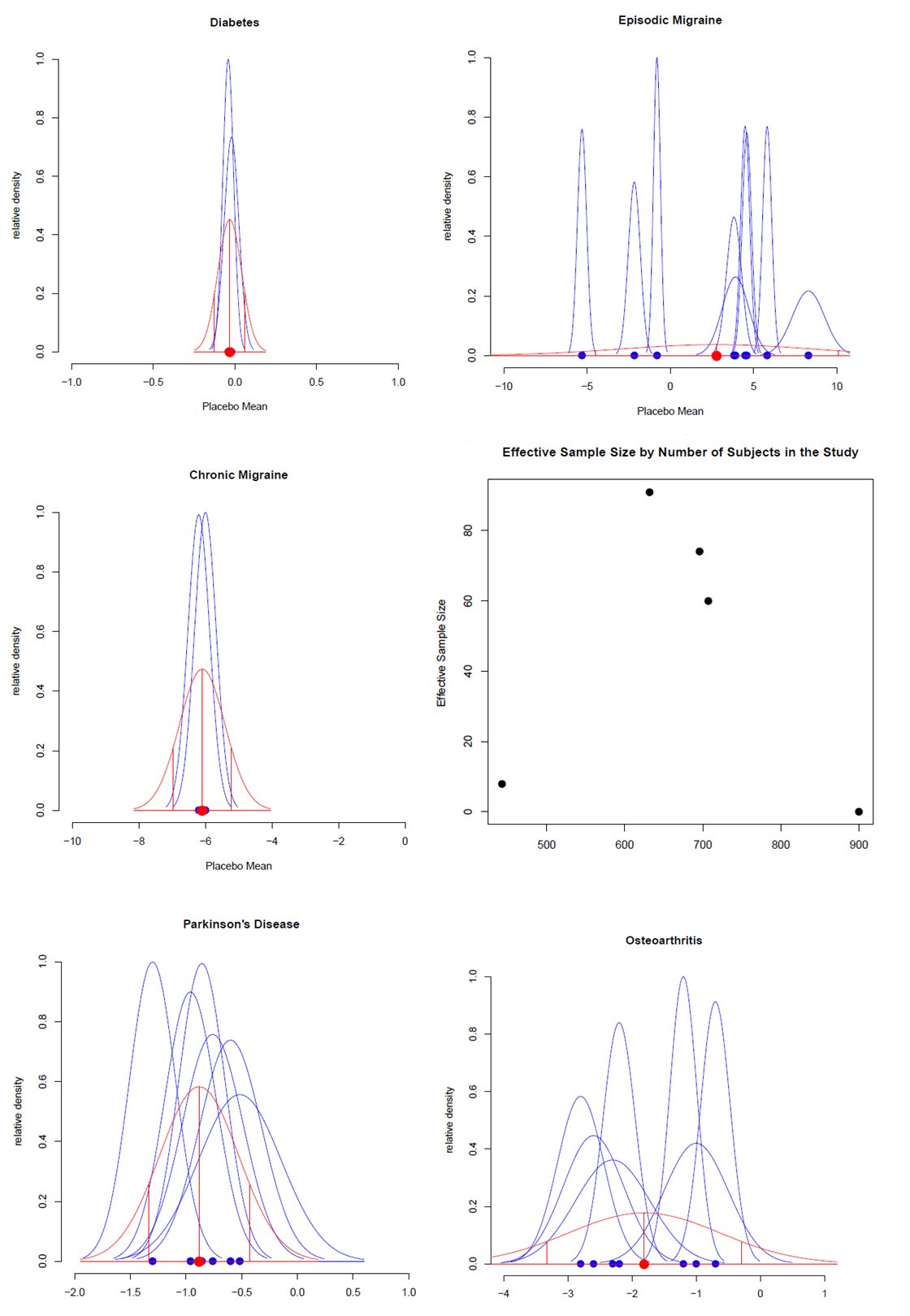
Five case studies of effective sample size (ESS) derived via utilizing an informative prior are presented. Prior data was gathered by a thorough review of the literature, seeking studies with similar design, subjects under study, and comparable outcome measures. The mean and SE were summarized for each study and the between subjects SD was calculated via a pooled SD.
ESS= (Between Subjects SD/ SD of Informative Prior)2
The informative prior was calculated via BugsXLA (an add in to Microsoft Excel which interfaces with OpenBUGS). Three chains of 15,000 samples were run with 5,000 burn in samples. Data were not thinned.
For each case, historical data y1 to yh were assumed to have a normal likelihood:
yh ~ N[θh, σ2h]
θh (h=1,…,H) and θ are assumed to be exchangeable so that, θh, θ ~ N(µ, τ2).
The analysis of the literature data used a non-informative prior N(µ=0, σ2= 1000), and modelled study as a random effect as N(µ=0, τ2= the 95th percentile of the maximum difference between studies).
The resulting posterior was plotted and the posterior SD were used in the calculation of the ESS.
Conclusions
Main Influences on ESS:
- Consistency of prior studies
- Standard error of outcome variable
- Sometimes, despite abundant literature, ESS may be low if studies are inconsistent.
- In such cases, this work is still important, as the study team should understand the outcome measure under study and be able to place it in appropriate context with past studies.
- Even if ESS is low, construction of an informative prior allows Bayesian analysis on the outcome of the study.
Results
Request a Consultation
References
Moate R (2012) Bayesian Study Design: The Pragmatic Approach to Phase II Trials. White Paper from Quanticate, Ltd.
Spiegelhalter et al (2004) Bayesian Approaches to Clinical Trials and Health-Care Evaluation. Woodward P (2011) Bayesian Analysis Made Simple. An Excel GUI for WinBUGS. Chapman & Hall/CRC Biostatistics Series.



